Daftar Isi
Pola Bilangan Gambar | TPS SBMPTN
Pelajari materi tentang pola bilangan gambar atau tebak bilangan dalam gambar untuk TPS SBMPTN di Les Privat SBMPTN beserta contoh soalnya.
Pengertian Pola Bilangan Gambar
Pola bilangan adalah suatu susunan bilangan yang memiliki bentuk teratur atau suatu bilangan yang tersusun dari beberapa bilangan lain yang membentuk suatu pola. Serta terdapat banyak jenis dan macamnya.
Rumus Pola Bilangan Gambar Berdasarkan Jenisnya
Suatu bilangan yang disusun akan membentuk suatu pola. Nah, susunan polanya bisa berupa bilangan ganjil-genap, aritmatika, geometri, persegi, persegi panjang, segitiga, fibonacci, dan bilangan pascal.
Simak penjelasan dari jenis-jenis pola bilangan gambar berikut ini:
Pola Bilangan Ganjil
Pola bilangan ganjil adalah susunan yang dimulai dari bilangan 1 sampai tak terhingga, tetapi merupakan angka ganjil. Contoh bilangannya adalah 1, 3, 5, 7, 9, dan seterusnya. Kalau menggunakan rumus yaitu:
Un = 2n – 1
Pola Bilangan Genap
Berbanding terbalik dengan pola bilangan ganjil, kalau pola bilangan genap merupakan susunan dari bilangan yang habis dibagi 2. Contoh bilangannya adalah 2, 4, 6, 8, 10, dan seterusnya. Seperti ini rumusnya:
Un = 2n
Pola Bilangan Aritmatika
Pola bilangan aritmatika adalah bilangan yang susunannya memiliki selisih tetap antar kedua sukunya. Contoh bilangannya seperti pada kasus pedagang kue di awal tadi, yaitu 8, 16, 24, 48, dan seterusnya (a = 8, b = 8). Ini dia rumusnya:
Un = a + (n-1)b
Keterangan:
a : suku pertama dari susunan bilangan
b : beda atau selisih
n : urutan bilangan ke-n
Pola Bilangan Geometri
Pola bilangan geometri adalah susunan bilangan yang membentuk pola dengan rasio selalu tetap antar kedua sukunya. Nah loh, gimana tuh? Langsung aja aku kasih contoh bilangannya yaitu 2, 6, 18, 54, dan seterusnya. Dari susunan bilangan tersebut, kira-kira rumusnya bagaimana ya? Rumusnya adalah:
Un = arn-1
Keterangan:
a : suku pertama dari susunan bilangan
r : rasio
n : urutan bilangan ke-n
Pola Bilangan Persegi
Pola bilangan persegi adalah susunan bilangan yang polanya seperti persegi, sehingga dibentuk oleh bilangan kuadrat. Rumus polanya yaitu Un = n2. Contoh susunan bilangannya adalah 1, 4, 9, 16, dan seterusnya.
Pola Bilangan Persegi Panjang
Hampir sama seperti sebelumnya, tapi rumusnya berbeda jauh lho, guys. Kalau ini akan menghasilkan bentuk menyerupai bangun datar persegi panjang. Contoh susunan angkanya adalah 2, 6, 12, 20, dan seterusnya. Kalau dituliskan dalam bentuk rumus akan seperti ini: Un = n (n+1).
Pola Bilangan Segitiga
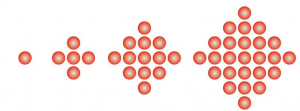
Dari namanya, kita udah bisa langsung menebak kalau pola bilangan ini akan membentuk bangun segitiga, betul atau betul? Nah, segitiga yang dimaksud di sini adalah bentuk segitiga sama sisi. Coba perhatikan gambar di bawah ini:
Pada gambar di atas, bilangan tersebut membentuk pola segitiga yang kalau dirumuskan akan diperoleh Un = ½ n (n+1). Kamu bisa cirikan suatu kelompok bilangan yang polanya seperti ini, bisa dikatakan bahwa bilangan tersebut membentuk pola segitiga. Contohnya adalah bilangan 1, 3, 6, 10, 15, dan seterusnya.
Pola Bilangan Fibonacci
Kalau yang satu ini kok namanya aneh ya, hmmm. Ternyata bilangan Fibonacci adalah susunan bilangan yang berawalan 0 dan 1, kemudian angka berikutnya diperoleh dengan cara menambahkan kedua bilangan sebelumnya secara berturut-turut. Contoh bilangannya adalah 0, 1, 1, 2, 3, 5, 8, 13, 21, dan seterusnya. Seperti ini aturan dan ilustrasinya:
Supaya lebih mudah, kamu bisa gunakan rumus berikut ini:
Un = (n – 1) + (n – 2)
Pola Bilangan Pascal
Terakhir, ada yang namanya pola bilangan Pascal. Mungkin banyak di antara kamu gak asing dengan nama Pascal. Yap, ditemukan oleh Blaise Pascal, seorang ilmuwan asal Prancis. Kita mengenalnya sebagai segitiga Pascal. Lalu, apa hubungannya dengan pola bilangan? Segitiga Pascal merupakan suatu pola bilangan. Kamu bisa melihatnya dari berbagai peraturan atau ketentuannya di sini:
- Baris paling atas ditulis satu kotak saja, yaitu 1.
- Setiap baris dalam segitiga pascal selalu diawali dan akan diakhiri oleh angka 1.
- Jumlah kotak selanjutnya dalam segitiga pascal ini ditulis di baris ke-2 sampai ke-n adalah hasil penjumlahan dua bilangan diagonal di atasnya.
- Setiap baris akan membentuk simetris.
- Banyak bilangan di setiap barisnya memiliki kelipatan dua dari jumlah angka baris sebelumnya.
Sangat unik, bukan? Supaya lebih terbayang, kamu bisa lihat gambar berikut ini ya.

Contoh Soal
Diketahui barisan bilangan 6, 18, 54, …, ….
Tentukan kelanjutan dari baris bilangan di atas!
Jawab:
Hal pertama yang harus kamu lakukan adalah dengan melihat selisih antar bilangannya.
6 → 18 → 54, selisih ketiga bilangan tersebut adalah x3.
Coba kita buktikan, 6 x 3 = 18, 18 x 3 = 54.
Berarti antar bilangannya memiliki pola x3, sehingga:
- 54 x 3 akan menghasilkan bilangan selanjutnya, yaitu 162.
- 162 x 3 akan menghasilkan bilangan selanjutnya, yaitu 486
Jadi, kelanjutannya adalah bilangan 162 dan 486.
Baca juga: Barisan dan Deret – Matematika SBMPTN
Nah, itu dia beberapa pemahaman mengenai pola bilangan gambar dalam TPS SBMPTN. Agar proses pembelajaran persiapan UTBK dan SBMPTN semakin efektif, mari belajar bersama Les Privat SBMPTN. Disini, para siswa akan mendapatkan kesempatan untuk belajar dengan guru les privat dan tutor yang mengasyikan, metode pembelajaran yang menyenangkan dan materi yang dikemas dengan seru. Cari tahu lebih lengkap mengenai Latis Education disini.